HEJNÝ: Hadi
“Hadi” jsou úlohy na procvičování matematických operací sčítání, odčítání, později i násobení a dělení.
[obrázek] Hejný M., Jirotková D., Slezáková– Kratochvílová J., učebnice Matematika pro 1/ II. díl pro ZŠ, 1.vydání, Plzeň, FRAUS, 2007, ISBN 978-80-7238-627-7
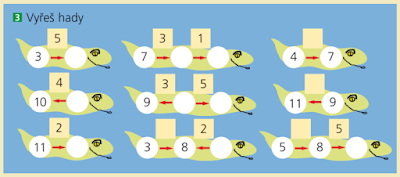
Čísla v bílých kruzích jsou stavy, čísla ve žlutých čtvercích umístěná nad červenými šipkami
jsou operátory změny.
Poznávání vazeb souborů čísel, která vystupují jak v roli vztahu, tak v roli operátora.
Zobecňování konkrétních poznatků.
Rozvíjení schopnosti řešit soustavu dvou rovnic metodou pokus – omyl.
Zdroj:
HEJNÝ, Milan, Darina JIROTKOVÁ a Jana SLEZÁKOVÁ-KRATOCHVÍLOVÁ. Matematika: pro 1. ročník základní školy- příručka učitele. 1. vyd. Plzeň: Fraus, 2007, 151 s. ISBN 978-807-2386-284, s.84, 88
MÁLKOVÁ, Pavlína. Příručka pro rodiče, 2014